PSO

PSO is Particle Swarm Optimization. A simple but powerful artificial intelligence field. In its simplest form, PSO is composed of a problem space with a certain solution or best position in it. Particles are scattered across this problem space. The particles each have a local fitness value according to their positions relative to the global best position. According to a simple algorithm displayed below, the particles evolve and begin to converge upon the solution to the problem in the problem space.

Algorithm:

Let there be n particles, each with associated positions and velocities , . Let be the current best position of each particle and let be the global best.

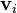• Initialize and for all i. One common choice is to take and for all i and , where a_j,b_j are the limits of the search domain in each dimension.
• and .

• While not converged:
  • For :
    • .
    • .
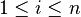    • If , .
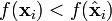    • If , .

Note the following about the above algorithm:

• ω is an inertial constant. Good values are usually slightly less than 1.
• c₁ and c₂ are constants that say how much the particle is directed towards good positions. They represent a "cognitive" and a "social" component, respectively, in that they affect how much the particle's personal best and the global best (respectively) influence its movement. Usually, we take but this need not be the case.
• are two random vectors with each compenent generally a uniform random number between 0 and 1.
• operator indicates element-by-element multiplication i.e. the Hadamard matrix multiplication operator.